用一次不等式或者一次方程式的形式来表示的几个制约条件下,求一次式中目标函数最大或最小的最优值的方法o作为最优化或作战计划(OperationsReserch,简称O.R)的方法被运用。
■求制约条件下的最大/最小值
线性规划法就是在满足“成本AW1000日元”的一次不等式或一次方程式所表示的制约条件下,求出使“销售额”目标函数最大化或最小化的变最(如销售量、电话外呼次数)的方法。
■曾被应用于第二次世界大战中
线性规划法始于第二次世界大战中美国、英国的作战计划。制定空中爆炸计划后,如果多添加轰炸机的燃料就能扩大行动范围,但是可以装载的炸弹数目就不得不减少;相反地,炸弹数目越多,可以装载的燃料就变少了。在这样的制约下,为了达到最佳的作战效果,计算燃料和炸弹的最佳装载量就成了线性规划法的起源。
■在高中数学里已经学过
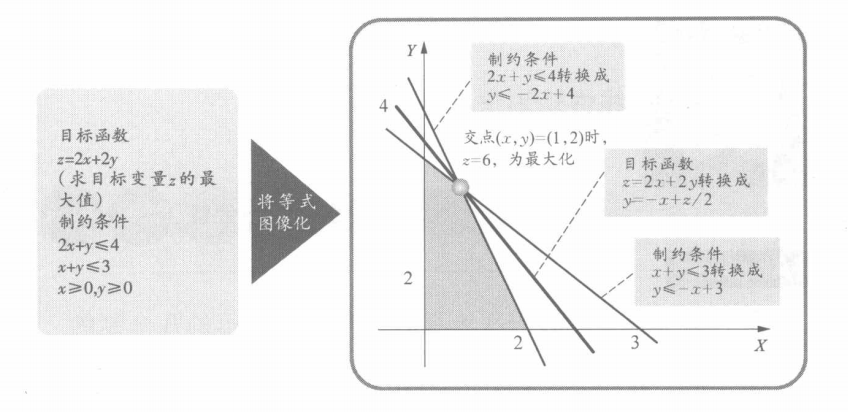
不喜欢公式的人大概对到此为止的解说敬而远之,但其实,简单的线性规划问题早已在高中数学中学过。不知道你对下页图还有印象吗?
■求制约条件下的最大/最小值
线性规划法就是在满足“成本AW1000日元”的一次不等式或一次方程式所表示的制约条件下,求出使“销售额”目标函数最大化或最小化的变最(如销售量、电话外呼次数)的方法。
■曾被应用于第二次世界大战中
线性规划法始于第二次世界大战中美国、英国的作战计划。制定空中爆炸计划后,如果多添加轰炸机的燃料就能扩大行动范围,但是可以装载的炸弹数目就不得不减少;相反地,炸弹数目越多,可以装载的燃料就变少了。在这样的制约下,为了达到最佳的作战效果,计算燃料和炸弹的最佳装载量就成了线性规划法的起源。
■在高中数学里已经学过
不喜欢公式的人大概对到此为止的解说敬而远之,但其实,简单的线性规划问题早已在高中数学中学过。不知道你对下页图还有印象吗?

如上图,先把制约条件的公式图表化,在符合制约条件的灰色区域里,用相符合的坐标值,代入目标函数,最后得到最大值和相应坐标。线性规划法将之进行了发展及应用,增加了变量和制约条件,能解决目标变量更为复杂的问题。
■线性规划法的应用领域
线性规划法是思考者本身可以算出数学最优解的简便方法,在众多领域中都有实际运用。如:
•军事、航天工业方面的“轨道计算问题“
•制造相关的“生产计划问题“
•物流业相关的“配送问题“
•医药业相关的“配制问题”
•电话外呼业相关的“清单计划问题“